Proof #1 (Euclid's Proof)
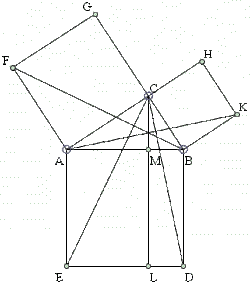
Hello! So this is Proof #1, and this proof involves congruent triangles and was originally created by Euclid.
So we have this right triangle and it's side's squares:
First of all, ΔABF = ΔAEC by SAS. This is because AE = AB (because ABDE is a square), AF = AC (because AFGC is a square), and
<BAF = <BAC + <CAF = <CAB + <BAE = <CAE. <CAE = <BAF.
So let's say triangle ABF has base AF and (if we extend line FA) the altitude from B is equal to AC (they are parallel). Its area then equals half that of square GFAC. On the other triangle, triangle AEC has AE (extended) base and the altitude from C equal to AM (C and M are both on line CL), where M is the point of intersection of AB with the line CL parallel to AE. So then the area of ΔAEC equals half that of the rectangle AELM (The base and height are the same as AELM's, so then 1/2 AELM = CAE). That says that the area AC*FA of the square on side AC equals the area of the rectangle AELM.
Similarly, the area BC*KB of the square on side BC equals that of rectangle BMLD. Finally, the two rectangles AELM and BMLD make up the square on the original right triangle's hypotenuse AB. So when you have 2 halves of 2 rectangles that make up a square, you get a half of a square. Then, since we started with 1/2 of the area of the triangles, 1/2a^2 + 1/2b^2 = 1/2c^2. Divide by 1/2 and you have the Pythagorean Theorem, a^2 = b^2 = c^2. QED
So we have this right triangle and it's side's squares:
First of all, ΔABF = ΔAEC by SAS. This is because AE = AB (because ABDE is a square), AF = AC (because AFGC is a square), and
<BAF = <BAC + <CAF = <CAB + <BAE = <CAE. <CAE = <BAF.
So let's say triangle ABF has base AF and (if we extend line FA) the altitude from B is equal to AC (they are parallel). Its area then equals half that of square GFAC. On the other triangle, triangle AEC has AE (extended) base and the altitude from C equal to AM (C and M are both on line CL), where M is the point of intersection of AB with the line CL parallel to AE. So then the area of ΔAEC equals half that of the rectangle AELM (The base and height are the same as AELM's, so then 1/2 AELM = CAE). That says that the area AC*FA of the square on side AC equals the area of the rectangle AELM.
Similarly, the area BC*KB of the square on side BC equals that of rectangle BMLD. Finally, the two rectangles AELM and BMLD make up the square on the original right triangle's hypotenuse AB. So when you have 2 halves of 2 rectangles that make up a square, you get a half of a square. Then, since we started with 1/2 of the area of the triangles, 1/2a^2 + 1/2b^2 = 1/2c^2. Divide by 1/2 and you have the Pythagorean Theorem, a^2 = b^2 = c^2. QED
